Two-level system
This page is intented as a reminder of useful formulas of the two level system in quantum mechanics. In particular Eq. \ref{Ufinalform}. Consider the following $2\times2$ hamiltonian:
\begin{align}
H=
\begin{pmatrix}
\varepsilon_1 & \Delta^* \\\
\Delta & \varepsilon_2
\end{pmatrix}.
\label{hamiltonian}
\end{align}
which can be rewritten as:
\begin{align}
H=\varepsilon\mathbb{1} + \vec d\cdot \vec \sigma.
\label{topoham}
\end{align}
by using the identity matrix $\mathbb 1$, the Pauli matrices vector $\vec \sigma$:
\begin{align}
\sigma_x =
\begin{pmatrix}
0 & 1\\\
1 & 0
\end{pmatrix},
\quad
\sigma_y =
\begin{pmatrix}
0 & -i\\\
i & 0
\end{pmatrix},
\quad
\sigma_z =
\begin{pmatrix}
1 & 0\\\
0 & -1
\end{pmatrix},
\end{align}
and the following definitions:
\begin{align}
\varepsilon&=\frac{\varepsilon_1+\varepsilon_2}{2},\\\
d_x&=\text{Re}\{\Delta\},\\\
d_y&=\text{Im}\{\Delta\},\\\
d_z&=\frac{\varepsilon_1-\varepsilon_2}{2}.
\end{align}
The eigenvalues of \eqref{topoham}, are:
\begin{align}
\boxed{
E_{\pm}
}
&=\varepsilon\pm|\vec d|
\\\
&=
\boxed{
\frac{\varepsilon_1+\varepsilon_2}{2} \pm \sqrt{ \Big(\frac{\varepsilon_1-\varepsilon_2}{2} \Big)^2 + \Delta^2}
},
\end{align}
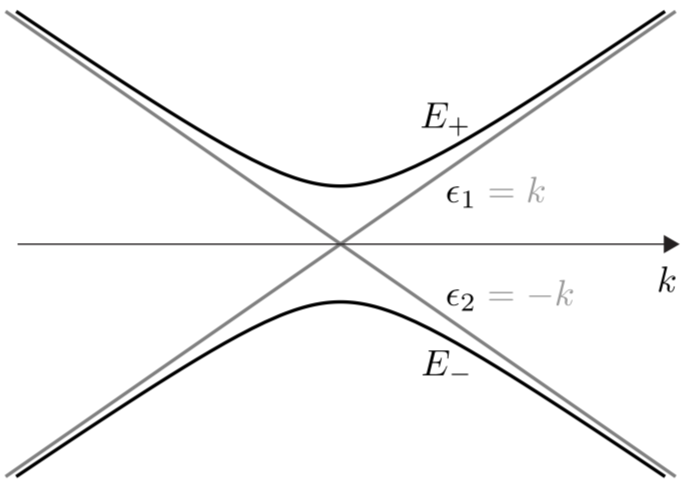
which are illustrated below, displaying the so-called "anti crossing".
The eigenvectors of \eqref{topoham} are the columns of the following unitary matrix: \begin{align} U= \begin{pmatrix} \cos \frac{\theta}{2} & -\sin \frac{\theta}{2}\\\ \text{e}^{\text i \phi}\sin \frac{\theta}{2} & \text{e}^{\text i \phi}\cos \frac{\theta}{2} \end{pmatrix}, \label{umatrix} \end{align} with the following definitions for $\theta$ and $\phi$: \begin{align} \cos \theta &= \frac{d_z}{|\vec d|} &= \frac{\frac{\varepsilon_1-\varepsilon_2}{2}}{\sqrt{ \big(\frac{\varepsilon_1-\varepsilon_2}{2} \big)^2 + \Delta^2}} \\\ \tan\phi &= \frac{d_y}{d_x} &\rightarrow \quad \Delta=|\Delta|\text{e}^{\text{i}\phi}. \end{align} Which can be simplified with half-angle identities: \begin{align} \sin \frac{\theta}{2} &= \pm\sqrt{\frac{1+\cos\theta}{2}} &\begin{cases} +\quad \text{if } 0\leq\frac{\theta}{2} < \frac{\pi}{2}\\\ -\quad \text{if } \frac{\pi}{2}\leq\frac{\theta}{2} < \pi\\\ +\quad \text{if } \pi\leq\frac{\theta}{2} < \frac{3\pi}{2}\\\ -\quad \text{if } \frac{3\pi}{2}\leq\frac{\theta}{2} < 2\pi \end{cases} \label{ineq1} \\\ \cos \frac{\theta}{2} &= \pm\sqrt{\frac{1-\cos\theta}{2}} &\begin{cases} +\quad \text{if } 0\leq\frac{\theta}{2} < \frac{\pi}{2}\\\ -\quad \text{if } \frac{\pi}{2}\leq\frac{\theta}{2} < \pi\\\ -\quad \text{if } \pi\leq\frac{\theta}{2} < \frac{3\pi}{2}\\\ +\quad \text{if } \frac{3\pi}{2}\leq\frac{\theta}{2} < 2\pi \end{cases} \label{ineq2} \end{align} noting that: \begin{align} \sqrt{\frac{1\pm\cos\theta}{2}} &= \sqrt{\frac{|\vec d|\pm d_z}{2|\vec d|} \times\bigg( \frac{|\vec d|\mp d_z}{|\vec d|\mp d_z} \bigg) } \\\ &= %\sqrt{\frac{|\vec d|^2 - d_z^2}{2|\vec d|^2\mp 2|\vec d|d_z} } %\\&= %\sqrt{\frac{|\vec d|^2 - d_z^2}{d_x^2+d_y^2+d_z^2+ |\vec d|^2\mp 2|\vec d|d_z} } %\\\ &= \sqrt{\frac{d_x^2+d_y^2}{d_x^2+d_y^2+(d_z \mp |\vec d|)^2} } \\\ &= \frac{|\Delta|}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{\mp})^2} }. \end{align} allowing to rewrite \eqref{umatrix} as: \begin{align} \boxed{ U=\begin{pmatrix} \frac{|\Delta|}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{+})^2} } & - \frac{|\Delta|}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{-})^2} } \\\ \frac{\Delta}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{-})^2} } & \frac{\Delta}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{+})^2} } \end{pmatrix} }. \label{Ufinalform} \end{align} Strictly speaking, the sign of each element in the matrix depends on which of $|\Delta|$ or $\frac{\varepsilon_1-\varepsilon_2}{2}$ is larger. Those quantities can be seen respectively as the opposite side and the adjacent side of the triangle defining $\theta$ in equations \eqref{ineq1} and \eqref{ineq2}. Finally, note the vector basis was defined so that \begin{align} \boxed{ U^\dagger HU = \begin{pmatrix} E_+ & 0\\\ 0 & E_- \end{pmatrix} }. \end{align}

The eigenvectors of \eqref{topoham} are the columns of the following unitary matrix: \begin{align} U= \begin{pmatrix} \cos \frac{\theta}{2} & -\sin \frac{\theta}{2}\\\ \text{e}^{\text i \phi}\sin \frac{\theta}{2} & \text{e}^{\text i \phi}\cos \frac{\theta}{2} \end{pmatrix}, \label{umatrix} \end{align} with the following definitions for $\theta$ and $\phi$: \begin{align} \cos \theta &= \frac{d_z}{|\vec d|} &= \frac{\frac{\varepsilon_1-\varepsilon_2}{2}}{\sqrt{ \big(\frac{\varepsilon_1-\varepsilon_2}{2} \big)^2 + \Delta^2}} \\\ \tan\phi &= \frac{d_y}{d_x} &\rightarrow \quad \Delta=|\Delta|\text{e}^{\text{i}\phi}. \end{align} Which can be simplified with half-angle identities: \begin{align} \sin \frac{\theta}{2} &= \pm\sqrt{\frac{1+\cos\theta}{2}} &\begin{cases} +\quad \text{if } 0\leq\frac{\theta}{2} < \frac{\pi}{2}\\\ -\quad \text{if } \frac{\pi}{2}\leq\frac{\theta}{2} < \pi\\\ +\quad \text{if } \pi\leq\frac{\theta}{2} < \frac{3\pi}{2}\\\ -\quad \text{if } \frac{3\pi}{2}\leq\frac{\theta}{2} < 2\pi \end{cases} \label{ineq1} \\\ \cos \frac{\theta}{2} &= \pm\sqrt{\frac{1-\cos\theta}{2}} &\begin{cases} +\quad \text{if } 0\leq\frac{\theta}{2} < \frac{\pi}{2}\\\ -\quad \text{if } \frac{\pi}{2}\leq\frac{\theta}{2} < \pi\\\ -\quad \text{if } \pi\leq\frac{\theta}{2} < \frac{3\pi}{2}\\\ +\quad \text{if } \frac{3\pi}{2}\leq\frac{\theta}{2} < 2\pi \end{cases} \label{ineq2} \end{align} noting that: \begin{align} \sqrt{\frac{1\pm\cos\theta}{2}} &= \sqrt{\frac{|\vec d|\pm d_z}{2|\vec d|} \times\bigg( \frac{|\vec d|\mp d_z}{|\vec d|\mp d_z} \bigg) } \\\ &= %\sqrt{\frac{|\vec d|^2 - d_z^2}{2|\vec d|^2\mp 2|\vec d|d_z} } %\\&= %\sqrt{\frac{|\vec d|^2 - d_z^2}{d_x^2+d_y^2+d_z^2+ |\vec d|^2\mp 2|\vec d|d_z} } %\\\ &= \sqrt{\frac{d_x^2+d_y^2}{d_x^2+d_y^2+(d_z \mp |\vec d|)^2} } \\\ &= \frac{|\Delta|}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{\mp})^2} }. \end{align} allowing to rewrite \eqref{umatrix} as: \begin{align} \boxed{ U=\begin{pmatrix} \frac{|\Delta|}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{+})^2} } & - \frac{|\Delta|}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{-})^2} } \\\ \frac{\Delta}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{-})^2} } & \frac{\Delta}{\sqrt{|\Delta|^2+(\varepsilon_1 - E_{+})^2} } \end{pmatrix} }. \label{Ufinalform} \end{align} Strictly speaking, the sign of each element in the matrix depends on which of $|\Delta|$ or $\frac{\varepsilon_1-\varepsilon_2}{2}$ is larger. Those quantities can be seen respectively as the opposite side and the adjacent side of the triangle defining $\theta$ in equations \eqref{ineq1} and \eqref{ineq2}. Finally, note the vector basis was defined so that \begin{align} \boxed{ U^\dagger HU = \begin{pmatrix} E_+ & 0\\\ 0 & E_- \end{pmatrix} }. \end{align}