Carrier density in a 2D antiferromagnet
In 2016, Badoux et al. showed that, in the high-temperature superconductor YBCO, the number of carriers measured by the Hall effect goes from $n_{H}=p$ to $n_{H}=1+p$ as a function of hole doping $p$. The suggested explanation for this phenomenon is an antiferromagnetic (AF) reconstruction of the Fermi surface. This suggestion was quantitatively explored by Storey, who demonstrated that it describes the $p$ to $1+p$ behaviour perfectly.
Here I want to clarify subtle aspects of this explanation. Let us start by dividing the number of carriers counted in the Brillouin zone in various ways.
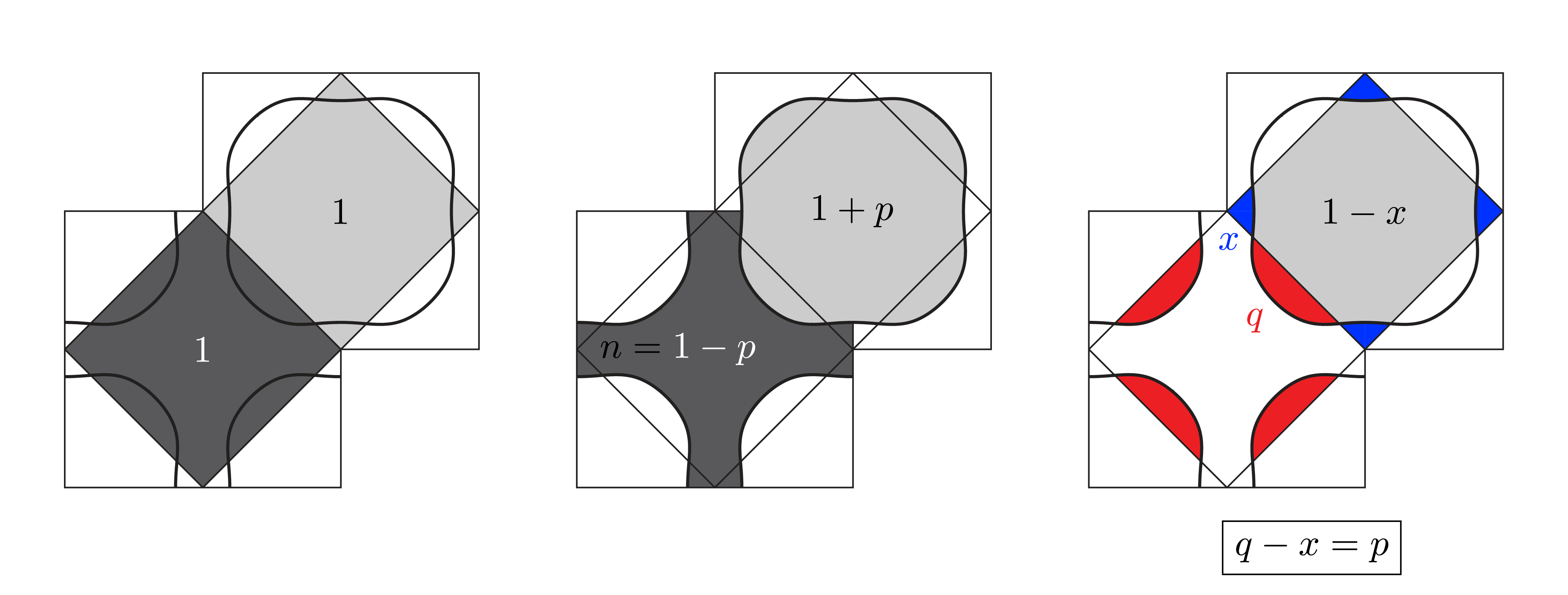
The left picture is to reminds that the Brillouin zone (BZ) contains 2 states per unit-cell of the lattice (one for each spin). We count one carrier in each reduced BZs of the AF reconstruction. In the middle picture, the hole doping is $p$, and we see that the Fermi surface splits the total volume of the BZ in $n=1-p$ electrons below the Fermi level, and $1+p$ holes above the Fermi level. This separation in $1-p$ and $1+p$ has nothing to do with the AF reduced BZs, it is strictly controlled by the doping of the sample. As you can see above, when considering the two divisions togheter, it is the difference between red portion and blue portion that give $p$.
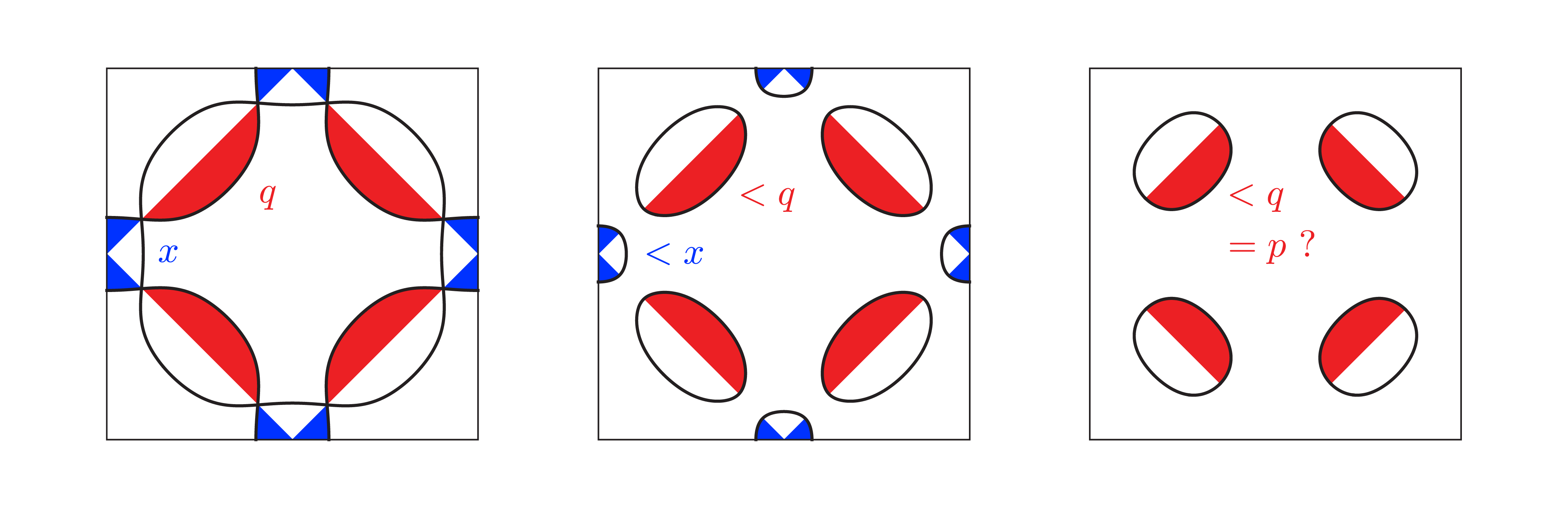
If we open the AF gap and keep the chemical potential fixed, both the red and blue volumes get smaller. For most band parameters, this results in a change of doping. In the AF mean-field picture, there is no garantee that these reductions cancel each other to preserve $p=q-x$. In fact, in computations, one needs to readjust the chemical potential for every value of gap considered, in order to find $p$ again in the reconstructed system. This is important: the carrier number is not $p$ because the pocket has a volume of $p$, it is $p$ because we want the doping in the whole system to be conserved.
The reason for which the Hall number goes from $1+p$ to $p$, in the AF scenario, is that the upper band, the one associated with the blue electon pockets, completely leaves the Fermi surface at some point. In other words, the single band with $1+p$ carriers loses $1$ entire carrier per unit-cell when undergoing the AF reconstruction. The leftover lower band, associated with the red hole pockets, contains $p$ carrier, not because the leftover volume is systematically $p$, but because we make it $p$, since we require doping $p$ in the whole two-band system.
In cuprates, antiferromagnetism does not extend as far in doping as where this change is observed, and thus this picture should not hold. However, if Mott physics is involved, there is a good chance that the split in two bands remains a good approximation to explain some experiments. What remains unclear, in that case, is if the upper band will remain a sharp band, or become incoherent spectral weight, and also if the bottom band will actually form a close pocket, or simply arcs. To my knowledge, these remain open questions.